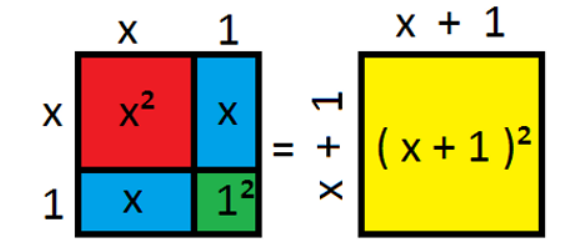Unit 1 - Polynomial Expressions
Click to set custom HTML
• In Grade 8, students begin to interpret algebraic expressions and parts of an expression in context.
• Students should be able to interpret parts of an expression, such as terms, factors, leading coefficient, coefficients, constant and degree in context.
• Given mathematically applicable situations, which utilize formulas or expressions with multiple terms and/or factors, students should be able to interpret the meaning of individual terms or factors within the given framework.
• Students should have opportunities to use polynomial expressions within the context of geometric shapes
• Students should be able to discuss the meaning of the variable in context, the degrees of the expressions and the sums/products.
• Students should understand that polynomials, like integers, are "closed" when it comes to addition, subtraction, and multiplication.
• Through investigation and exploration, students should be given opportunities to discover that the sum and/or difference of two or more polynomials is a polynomial and the product of two polynomials is a polynomial.
• Students should have opportunities to perform operations with binomials, trinomials, and other polynomials.
• A polynomial is any expression that is a combination of one or more monomials connected via addition or subtraction.
• Students should be able to use algebraic reasoning to show and explain how integers and polynomials are similar in that they both are closed under addition, subtraction, and multiplication.
• Students should have opportunities to perform operations with first-, second-, third-, fourth-, and fifth-degree polynomials.
• Students should be able to interpret parts of an expression, such as terms, factors, leading coefficient, coefficients, constant and degree in context.
• Given mathematically applicable situations, which utilize formulas or expressions with multiple terms and/or factors, students should be able to interpret the meaning of individual terms or factors within the given framework.
• Students should have opportunities to use polynomial expressions within the context of geometric shapes
• Students should be able to discuss the meaning of the variable in context, the degrees of the expressions and the sums/products.
• Students should understand that polynomials, like integers, are "closed" when it comes to addition, subtraction, and multiplication.
• Through investigation and exploration, students should be given opportunities to discover that the sum and/or difference of two or more polynomials is a polynomial and the product of two polynomials is a polynomial.
• Students should have opportunities to perform operations with binomials, trinomials, and other polynomials.
• A polynomial is any expression that is a combination of one or more monomials connected via addition or subtraction.
• Students should be able to use algebraic reasoning to show and explain how integers and polynomials are similar in that they both are closed under addition, subtraction, and multiplication.
• Students should have opportunities to perform operations with first-, second-, third-, fourth-, and fifth-degree polynomials.
Textbook Connections
Module 11-1 Areas of Quadrilaterals
Students will find areas of quadrilaterals by using the formulas they derive.
Module 11-1 Areas of Quadrilaterals
Students will find areas of quadrilaterals by using the formulas they derive.